ABOUT THE FABRIC OF SPACE-TIME
A. HOW TO REPRESENT THE COMPONENTS OF DIRECTION & SPACE-TIME
To begin, we need to review our current method of representing 3-dimensional space, both graphically & mathematically.
The most popular method of graphic representation is the 2D ISOMETRIC GRAPH,
depicting an (X,Y,Z) EUCLIDEAN SPACE using CARTESIAN (X,Y,Z) DISTANCE COORDINATES,
in "DIRECTIONS" all orthogonal to each other & shown as follows:
...........+ Y......Where X, Y, & Z are directions orthogonal
............ |..................to each other & each measured in units
.............| .................of distance.
.............|________________>+X The basic vector direction
............ /
...........-Z
Under this system, any point in space is represented mathematically & located by the set
of coordinates (X, Y, Z) all expressed in terms of linear distance.
But there is a problem with this system in that it falls short in being able to describe
TIME which is now considered a 4th dimension. Where we once only considered space to be
the ultimate reality, we now speak of SPACE-TIME. So we now ask "Is there anyway of including
TIME within our graphical & mathematical capabilities?". There was a mathematical answer to
this question a long time ago. We simply added another 4th ordinate to our coordinate
expression, ie, (X, Y, Z, T). But how can this MULTI-DIMENSIONALITY be represented in a
2-dimension graphic without getting really confused? That is what we seek to answer here.
Using our old standard 3-ORTHOGONAL AXIS GRAPHIC, instead of using linear distance
coordinates in all 3 orthogonal directions, let's look at using a MIX OF THE X-AXIS LINEAR DISTANCE
ORDINATE COUPLED WITH THE USE OF POLAR COORDINATES RESULTING FROM THE NUMBER OF
REVOLUTIONS OF A WHEEL TRAVELING ALONG THE Z-AXIS IN THE Z-Y PLANE.
First, we establish a basic (parent) vector direction corresponding to the axial spin direction established by a virtual spinning object.
This will be our old traditional linear distance ordinate X-AXIS or X-direction. Once we travel a
distance, d1, along the X-Axis, we intersect the relocated Z-Y (or Y-Z) PLANE. At this point
we now change how we get to the target point in the Z-Y PLANE by using POLAR COORDINATES.
Here is an example diagram depicting this situation, with instructions to go out +9 feet
along the X-AXIS (d1), turn left 90 degrees into the Z-Y plane, then look up 60 degrees(a)
& go 7 feet (d2) in that direction. We have effectively used polar coordinates to get to our
location in the Z-Y PLANE. Here is our isometric view.

But we still have 3 coordinates:
d1 = the distance along the X-AXIS,
a = the polar angle of the direction in which we travel d2 = distance.
Is there any way of expressing the two polar coordinates as just one variable along the Z-AXIS,
thereby allowing us to use the Y-AXIS to plot time, T?
Recongnizing that our X ordinate is always going to be in terms of linear distance, this means we
only need concern ourselves with what happens in the 2-dimensional Z-Y PLANE.
So here we rotate the Z-Y plane around the Y-AXIS to see it head-on.

It should be noted that d2 is the hypotenuse of a right angle, which means we can compute
the EQUIVALENT Z & Y CARTESIAN COORDINATES using simple plane geometry.
For the Y ordinate, d3 = d2 x Sine(a).
For the Z ordinate, d4 = d2 x Cosine(a)
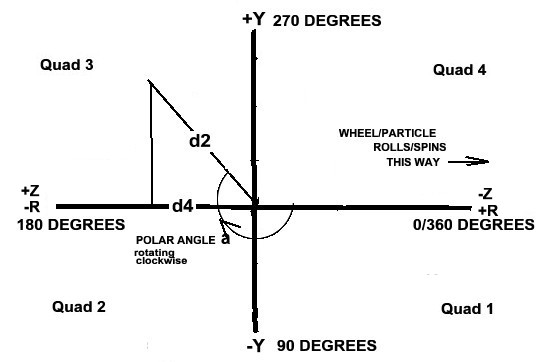
Let us now consider a wheel starting at the origin. We put a mark on the wheel point in the
direction of the +Z-AXIS. We now roll the wheel along the Z-AXIS & travel distance d4.
The distance is computed , d4 = 2 x PI x Wheel-Radius (r) x # Of Revolutions (R). It should
be obvious that if the wheel turns a whole number of revolutions, then our original direction
mark on the wheel is pointing exactly in the same direction as the Z-AXIS, which will mean
there is no Y-coordinate. On the other hand, If the wheel turns a whole number of revolutions
plus some fraction of a whole turn other than 1/2, then there will be a Y-coordinate. We now
note that when there is a partial turn =
1/8 of a revolution, then
it = 45 polar degrees from +Z into the +Z -Y quadrant 1.
1/4 of a revolution, then
it = 90 polar degrees in the -Y direction. Z = 0.
3/8 of a revolution, then
it= 135 polar degrees into the -Z -Y quadrant 2.
1/2 of a revolution, then
it = 180 polar degrees in the - Z direction. Y = 0
5/8 of a revolution, then
it = 225 polar degrees into the -Z +Y quadrant 3 .
3/4 of a revolution, then
it = 270 polar degrees in the +Y direction. Z = 0
7/8 of a revolution, then
it = 315 polar degrees into the +Z +Y quadrant 4 .
At this point, you might be saying "Wait a minute. You moved the wheel a linear distance along the Z-AXIS
to obtain the angle in the direction at which to look, BUT YOU HAVE NO LINEAR DISTANCE TO TRAVEL
IN THAT DIRECTION TO LOCATE THE FINAL POINT". To answer that concern, we have to bring in some
tricky parts. Instead of visualizing the wheel as moving away from the origin, let's assume the center of
the wheel is fixed along the X-AXIS and the Z-AXIS is moving under the wheel at a radial distance r,
the radius of the wheel. Hence when the Z-AXIS stops moving the distance d4, we now are able to refer
to a unique & specific point in space via POLAR COORDINATES. But there is one more little trick to
increase the accuracy of our distance measurement. THE RADIUS, r, NEEDS TO BE AS SMALL AS POSSIBLE IN
TERMS OF THE BASIC UNIT OF MEASURE ALONG THE X-AXIS. IN OTHER WORDS, THE VALUE OF r
NEEDS TO APPROACH 0, BUT NOT QUITE - MAYBE EVEN THE SIZE OF A SPINNING ATOMIC PARTICLE.
THIS GIVES US WHAT AMOUNTS TO A DIGITAL-LIKE MEASUREMENT OF DISTANCE ALONG THE
Z AXIS. AND WE CAN NOW COMPUTE THE POLAR DISTANCE ORDINATE TO BE
d2 =| d4 / cos(a)| , Where d4 = 2 x PI x r x R. It should be noted that, rotating in a clockwise
manner, the values of the cosines of the polar angles between 90 degrees & 270 degrees are the
negatives of the cosine values of angles between 270 & 90 degrees. In addition, were we to place the
Z-AXIS over the wheel instead of under the wheel, we would be getting a negative distance as opposed to
a positive distance along the Z-AXIS. But this is unimportant when using polar coordinates, because
we are only interested in the absolute value of the distance traveled along the Z-AXIS, d4, in order
to compute the absolute value of the distance traveled in the polar direction indicated by the
wheel, d2. Therefore, it is unnecessary to be concerned about which quadrant to which any partial
revolution points or whether or not our revolution origin should begin along the vertical axis as opposed
to the horizontal axis, or whether or not we place the Z-AXIS on top of our wheel or on the bottom,
the later being our choice in this discussion.
Thus, we can finally map every point in the Z-Y (or Y-Z) plane using polar coordinates based solely upon the
NUMBER OF REVOLUTIONS, R, that a particle spins, WHICH BECOMES A NEW UNIT
OF MEASURE THAT REPLACES THE DISTANCE COORDINATES, (Z,Y) & WHERE THE
DIRECTION OF +R IS 180 DEGREES AWAY FROM THE DIRECTION OF +Z.
Here is our isometric view.

Rotating the Z-Y PLANE to see it head on, we have:
So we can now represent the (X,Y,Z) coordinates of space as just two cordinates, (X,R).
This means we can replace the Z-AXIS with a new NUMBER OF REVOLUTIONS R-AXIS, & graphically free
up the use of the Y-AXIS replacing it with a new TIME T-AXIS as shown below.
(NOTE: There is nothing to say if TIME is, or is not, orthogonal to the other dimensions.
But for simplicity of drawing, we assume it is.)
In addition, WE MUST NOT CONFUSE THE Z-Y (or Y-Z) PLANE WITH THE NEW R-T (or T-R) PLANE.
In making this replacement, we have hidden the X,Y,Z (or X-R) EUCLIDEAN SPACE from view
& created a new X,R,T, EUCLIDEAN SPACE. It's like changing the channel on your tv.
But we note that the X-AXIS is COMMON TO BOTH THE X,Y,Z & X,T,R EUCLIDEAN SPACES.
So there is a link (or connection) between the two spaces. Here is our isometric view.

Finally, looking straight on to the rotated R-T PLANE:

In terms of mathematical coordinates, these would show as (X, Revolutions, Time) or simply (X,R,T).
And this is how we can represent the 4 dimensions in a 3-dimensional reference system
graphically represented in 2-dimensions.
B. INTERPRETATIONS:
First of all, I am quite sure that minds far brighter than mine have already come up with this
stuff, given that some sub-atomic particles are identified by their "SPIN" in quantum mechanics,
& that "MATRIX MATH, MULTI-DIMENSIONAL MATRICES MATH, VECTOR MATH, & STRING THEORY have evolved
far beyond my understanding at this time. But this should help the lay person (myself included)
at least begin to understand what more advanced theorists are talking about. So I beg your
continued indulgence as I try to interpret the meanings of these new EUCLIDEAN VECTOR SPACES.
1. FOCUSING ON THE X-R PLANAR SPACE, THE R-AXIS.
a. A WORD ABOUT TRANSCENDENTAL & IRRATIONAL NUMBERS.
It should be noted that in replacing the Y & Z distance ordinates with R, the number of revolutions
of a wheel of radius, r, we have introduced the use of PI which is a transcendental number.
A TRANSCENDENTAL NUMBER is a number that is not the root of any integer polynomial,
meaning that it is not an algebraic number of any degree. Every real transcendental number must also
be irrational, since a rational number is, by definition, an algebraic number of degree one.
But the converse is not true. There are some irrational numbers that are not transcendental.
PI (the ratio of circumference to diameter), e (eulers constant), & i (the sq root of -1) are all "transcendental".
The definition of an IRRATIONAL NUMBER is a number, using any integer based number system,
for which there exist no integers p and q such that the ratio between p and q is the desired number.
All rational numbers can be expressed as fractions of integer numbers. Not so with irrational numbers.
It is the fractional part of an irrational number that makes it irrational. It is
the part that can no longer be divided. It is the part that is less than unity & in no way
relates to unity. It stands by itself & can never be approached. There is no smallest positive rational
number, because if there were, then it could be divided by two to get a smaller number. Irrational numbers
must not be construed to simply be those numbers that have an unending decimal point. For example
take the number .333333..... & on, which is the result of dividing 1 by 3. The question is,
"CAN YOU EVER LAND EXACTLY ON THIS NUMBER?". The answer is, "YES, IF YOU ARE IN A BASE 3
NUMBER SYSTEM WHERE 1 DIVIDED BY 3 = .1 EXACTLY WITH NO UNENDING SEQUENCE".
REAL NUMBERS include both rational & non-imaginary irrational numbers, but not imaginary numbers.
Presumably, real numbers can be thought of as points along a line. But this is what I am challenging.
With respect to the math of irrational numbers, we note that:
1] A rational number times an irrational number results in an irrational number.
But PI is irrational. Therefore, the circumference of a perfect circle, C = 2 * r * PI is irrational.
Fractions are rational numbers. Therefore, any fractional part C is irrational.
The points around the circumference of a circle are a mixture of rational with irrational distances.
The only way to make a circle's circumference rational is to choose a radius that is irrational.
But this is an impossibility in the real physical world.
2] An irrational number times an irrational number may, or may not, result in an irrational number.
there are some cases where an irrational times an irrational results in a rational number.
3] The square root of a prime number is always irrational.
4] An irrational + an irrational may be either rational or irrational.
5] An irrational + a rational is always irrational.
6] PLANCK LEGTH = 1.6 X 10**(-35) METERS. PLANCK TIME = 10**(-43) SEC.
b. WHAT IS VIRTUAL SPACE IN THE "FABRIC" OF SPACE?
In REAL SPACE you cannot go an irrational distance via linear measurement. This might seem
to be contradicted by fact that we all know that we can travel a rational linear distance on
our car wheels. So how can we say this? The fact is our car wheel is not a "perfect" circle.
Some may argue that they can make the perfect circle (or wheel) by rotating a fixed linear
distance about a fixed point. But the fact is there are microscopic errors in that process.
The fact is it is physically impossible to create the perfect circle. The perfect
circle is a "virtual" entity, not a real one. Our car wheel is only an approximation.
When it comes to measuring REAL DISTANCES (or lengths), the unit of measure must be a rational
number, because YOU CAN NEVER TRAVEL AN IRRATIONAL DISTANCE FOR WANTING TO GET TO IT &
WITHOUT SKIPPING OVER IT. It is physically impossible.
This means that the "perfect" circle is an "IRRATIONAL NUMBER GENERATOR", the revolutions
of which can be used as a unit of measure to virtually map the points in space that are
irrational, even though we can never physically get to them. Depending upon the real linear
length of the circle's radius, r, if r is
extremely small relative to the unit of linear distance measure, then there will be more
irrational numbers per normal unit linear distance traveled than if r is extremely large.
When the unit of measure is an inch, a car wheel is extremely large as compared to an atomic
particle size. And so, when using inches as a unit of measure it might seem there are far
more rational distances than irrational distances traveled by the car wheel as it unwinds
along its linear path. We simply ignore the existence of irrational distances. An old joke
went, the difference between a mathematician & and an engineer has to do with trying to
reach Marilyn Monroe by going half the distance to her, then half the distance again, & so
on. The mathematician would say that he would never reach her. The engineer would say that
he could reach her for all practical purposes.
No matter, that does not alter the fact of the existence of irrational virtual points along
the path traveled, which leads us to conclude that these irrational virtual points must form
a VIRTUAL SPACE that is intertwined with REAL SPACE. VIRTUAL SPACE is that in which distances
can be computed by the number of complete revolutions, R, of a perfect wheel of a very small
radius, r, but NOT MEASURABLE BY A LINEAR RULER. It is physically impossible to exactly
locate a point when it is an irrational distance from the REAL POINT of origin. Therefore,
VIRTUAL SPACE is comprised of all points located at an irrational distance from the real point
of origin & interspersed with REAL SPACE. It is as if the "template" of real space was
overlayed with the "template" of virtual space, with possibly "time" being the
separator between the two.

To recap,
1] ALL REAL DISTANCE MEASUREMENTS MUST BE RATIONAL NUMBERS IN REAL-SPACE.
2] ALL IRRATIONAL NUMBERS ARE IN UNREACHABLE VIRTUAL SPACE, REPRESENTING IRRATIONAL POINTS IN
SPACE-TIME THAT CAN ONLY BE SKIPPED OVER IN THE REAL-SPACE OF SPACE-TIME.
3] REAL-SPACE & VIRTUAL-SPACE APPEAR TO BE INTERTWINED, BUT MAY BE SEPARATED BY TIME.
4] POINTS IN VIRTUAL-SPACE ARE BEST REPRESENTED IN TERMS OF CIRCULAR REVOLUTIONS RATHER THAN LINER
DISTANCES.
THE R-X PLANAR SPACE.
..R. (Revolutionary Irrational VIRTUAL Distances)
...|
...|..........p = Any point located in this space (X,R)
...|
...|-------------------X (Linear .Rational REAL distances)
...Origin
5] In addition, to REAL SPACE & VIRTUAL SPACE, there may be an IMAGINARY SPACE which would be
comprised of all imaginary numbers, ie, the square root of negative numbers. So it might be said
that TOTAL SPACE INCLUDES REAL SPACE, VIRTUAL SPACE, & IMAGINARY SPACE.
Why is this important?
Scientist and mathematicians of today are talking about the "FABRIC OF SPACE-TIME".
They are telling us that there is a "quantum world" consisting of more than time & 3 dimensions.
They are telling us that there are sub-atomic particles having the property of "SPIN".
They are telling us that space-time is malleable & impacted by gravity. T
hey are telling us that there exists a "dark matter", 'black holes" & "dark energy".
We do not dispute the scientists. They have plenty of evidence to support their claims.
But in order to understand that "fabric", we need to know exactly what the components of space really might be
& how to locate & view them. The world of numbers & proportions might not solve everything.
But they certainly help. We may come to find that the infinitesimal has some very large consequences.
WHAT ARE THE IMPLICATIONS FOR SCIENCE?
WITH RESPECT TO NANO SIZES,
ENTER THE HEISENBERG UNCERTAINTY PRINCUPLE & QUANTUM MECHANICS PROBABILITY MATH.
WITH RESPECT TO MACRO SIZES,
IT MAY BE THAT THE DARK MATTER & ENERGY, THAT WE SAY IS THERE, IS ACTUALLY IN IRRATIONAL
OR IMAGINARY SPACE.
IT MAY BE THAT TIME IS WHAT SEPARATES REAL-SPACE FORM THE VIRTUAL SPACE OF IRRATIONAL NUMBERS.
2. WHAT ABOUT THE R-T PLANAR SPACE.
Looking at the new R-T (or T-R) PLANE at a distance x along the X-AXIS, it would seem that
any point in the R-T PLANE would simply be REVOLUTIONS PER UNIT OF TIME, COMMONLY MEASURED
AS "RPM". However, what if either T or R are equal to 0? If T=0, can we really have any R?
It is an intriguing question, especially when we consider that sub-atomic particles are said to have "SPIN".
�